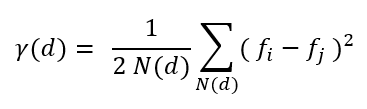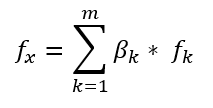Kriging – wenn es um jeden Datenpunkt geht!

Theorie

Überblick

Kriging ist eine Methode der räumlichen Interpolation, die ihren Ursprung im Bereich des Bergbaus hat und nach dem südafrikanischen Bergbauingenieur Danie Krige (1951) benannt ist. Die mathematische Grundlage wurde 12 Jahre später vom französischen Mathematiker Georges Matheron entwickelt.

Beschreibung

Kriging ist eine von mehreren Methoden, die eine begrenzte Anzahl von Datenpunkten verwenden, um den Wert einer Variablen in einem kontinuierlichen räumlichen n-dimensionalen Feld zu schätzen. Ein Beispiel für einen Wert, der über ein zufälliges räumliches Feld variiert, könnte die durchschnittliche monatliche Temperatur an bestimmten Orten sein. Es unterscheidet sich von einfacheren Methoden wie der abstandsgewichteten Interpolation oder der linearen Regression dadurch, dass es bei Kriging angenommen wird, dass der Abstand oder die Richtung zwischen Referenzpunkten eine räumliche Korrelation widerspiegelt, die zur Beschreibung von Veränderungen der gesuchten Funktion herangezogen werden kann. Das Krigingmodell ist eine mathematische Funktion für eine bestimmte Anzahl von (Stütz-)Punkten innerhalb eines bestimmten Radius, das einen Funktionswert für alle Richtungen und Entfernungen angibt.

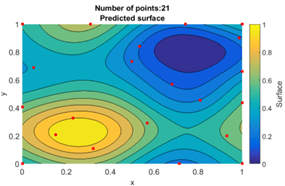
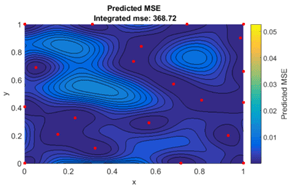
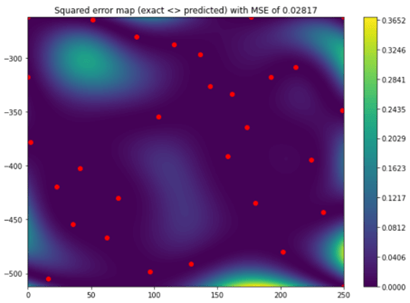
Abb 1: Links Darstellung der untersuchten Funktion mit den ausgewerteten Stützpunkten (rot). Rechts der vorhergesagte mittlere quadratische Fehler des Models.

Im Allgemeinen wird das Krigingmodell so berechnet, dass Punkte, die sich in der Nähe des untersuchten Ortes befinden, stärker gewichtet werden als weiter entfernte Punkte. Die Clusterbildung von Punkten wird ebenfalls berücksichtigt, so dass Punktcluster weniger stark gewichtet werden, denn sie enthalten weniger Informationen als einzelne Punkte.

Kriging ist ein mehrstufiger Prozess, der eine

• statistische Analyse der Daten,
• die Modellierung von Variogrammen,
• die Erstellung von Funktionsmodellen
• und (optional) die Untersuchung des Erwartungsfehlers umfasst.

Das Variogramm

Ein Variogramm (manchmal auch „Semivariogramm“ genannt) ist eine visuelle Darstellung der Varianz zwischen den einzelnen Punktpaaren in den Stichprobendaten. Für alle Punkte N(d) im Abstand d wird der Gamma-Wert γ(d), ein Maß für die mittlere quadratische Differenz zwischen ihren Werten , gegen den Abstand d zwischen ihnen aufgetragen.

Für die so ermittelten Varianzwerten wird eine Fitfunktion berechnet, die im Modell für die Abschätzung der Varianz an den nicht untersuchten Abständen abgibt. Die Fitfunktion wird aus den sich gut etablierten Funktionen manuell oder durch die Bestimmung der kleinsten Abweichung ausgewählt.

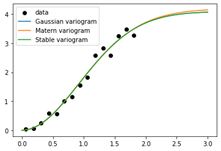
Abb 2: Beispiel für die gefitteten unterschiedlichen theoretischen Variogrammmodelle (Gaussian, Matern, Stable, hier Gaussian identisch mit Stable) anhand des experimentellen Variogramms (schwarze Punkte)

Die Kriging-Gewichte

Die Gewichte für jeden interpolierten Punkt werden entsprechend der räumlichen Struktur des interpolierten Ortes im Verhältnis zu allen Stichprobenpunkten berechnet. Die Gewichte werden aus dem Variogramm auf der Grundlage der räumlichen Struktur der Daten (Kovarianzmatrix) nach der folgenden Formel (hier vereinfacht) ermittelt:

wobei der Wert des vorhergesagten Punktes gleich der Summe des Wertes jedes abgetasteten Punktes mal der eindeutigen Gewichtung dieses Punktes ist:

Arten von Kriging

Es gibt mehrere Untertypen des Krigings, die bekanntesten darunter sind:

Ordinary Kriging, ist die gebräuchlichste und am weitesten verbreitete Kriging-Methode und wird standardmäßig verwendet. Dabei wird davon ausgegangen, dass der Mittelwert des Erwartungsfehlers nicht bekannt ist.

Universal Kriging, hierbei wird davon ausgegangen, dass es einen dominanten Trend in den Daten gibt und dass dieser durch eine deterministische Funktion, das Polynom, modelliert werden kann. Der so bestimmte Trend wird aus den ursprünglich gemessenen Punkten extrahiert. Nach der Bestimmung des Modells wird das Polynom wieder zu den Vorhersagen hinzugefügt, um trendbasierte Ergebnisse zu erhalten. Universal-Kriging sollte nur dann verwendet werden, wenn die Annahme eines Trends in den Daten wissenschaftlich oder empirisch belegt werden kann.

Simple Kriging … und mehr.

Anwendungsbeispiel

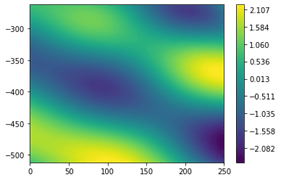
1. Modellerstellung folgender 2D-Funktion

Abb 3: Plot der zu interpolierenden Funktion

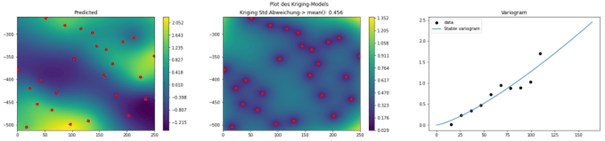
2. Berechnung des Krigings-Modelles mit n=25 Stützpunkten

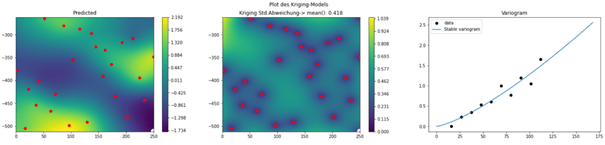
Abb 4: Auswahl der ersten Stützpunkte (rote Punkte, hier n=25), Berechnung des Variogramms (rechts), Darstellung der vorhersagten Funktion (links) mit dem zugehörigen Erwartungsfehler des Modells (Mitte)

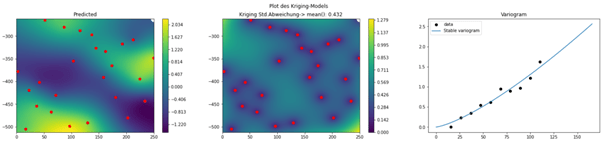
3. Erweiterung und Neuberechnung des Modelles um weitere 5 Stützpunkte an der Stelle des max. Fehlers

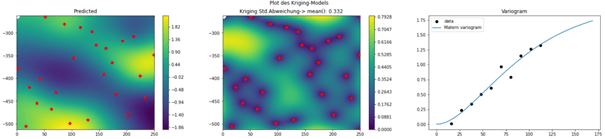
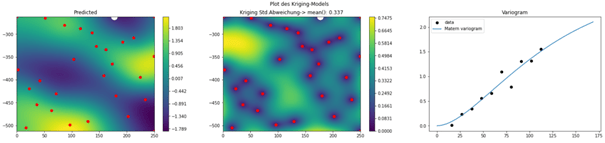
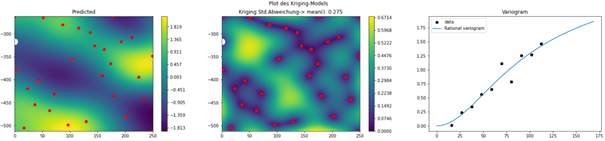
Abb 5: Sukzessive Erweiterung des Modells um einen zusätzlichen Punkt (weiß) an der Stelle des maximallen Modellfehlers (beachte Skalierung) mit anschließenden Neuberechnung des Variogramms (rechts), die Antwortfunktion (links) und der zugehörige Erwartungsfehler des Modells (Mitte)

4. Endmodell mit 30 Stützpunkten

Abb 6: Der mittlere quadratische Fehler des Modells im Vergleich zur wahren Funktion (Im Normalfall nicht bekannt, hier zur Validierung dargestellt)

Take-home message

Die Kriging-Methode ist eine verbreitete Interpolierungsmethode, die Anwendung in unterschiedlichsten Bereichen findet, in denen geringe Anzahl an Messpunkten vorliegen bzw. die Bestimmung neuer Messpunkte zeit- oder kostenintensiv ist. Insbesondere die Vorhersage des Modellfehlers ermöglicht es eine bestmögliche Verbesserung des Modelles zu erzielen, indem die Funktion an den entsprechen Stellen ausgewertet wird. Diese Eigenschaften können zur Bewertung und Optimierung anderer Modelle genutzt werden.
Es steht dem Leser zum Themavertiefen ein Jupyter-Notebook mit Verständnisaufgaben bereit:
https://github.com/prodato-alexander/kriging

Quellenverzeichnis

• Columbia University Mailman School of Public Health, Kriging-Interploation, June 7, 2022
• Georges Matheron, Principles of geostatistics, Economic Geology (1963) 58 (8): 1246–1266.
• Auchincloss, A. H., Diez Roux, A. V., Brown, D. G., Raghunathan, T. E. & Erdmann, C. A. Filling the gaps: spatial interpolation of residential survey data in the estimation of neighborhood characteristics. Epidemiology18, 469–478 (2007). (This study uses a variety of spatial interpolation methods, including kriging, to estimate the availability of healthy foods across neighborhoods using a limited set of sampled data).
• https://en.wikipedia.org/wiki/Kriging, Januar 9, 2023
• Jack P.C. Kleijnen, Kriging metamodeling in simulation: A review, European Journal of Operational Research, Volume 192, Issue 3, 2009, Pages 707-716, ISSN 0377-2217,
• Royle, A. G., F. L. Clausen, and P. Frederiksen. „Practical Universal Kriging and Automatic Contouring.“ Geoprocessing 1: 377–394. 1981.
• https://github.com/prodato-alexander/kriging